Extending the Linear Model
This is a lab script will encourage you to not overthink the linear model. If you’re comfortable with what it’s telling you in the simple bivariate case, extending it to include other complexities (like interactions, fixed effects, or other inputs) is a really simple matter. Multiple regression partials out effects of other variables on the dependent variable. Don’t sweat it too much..
R Packages/Data for This Session
You should’ve already installed the R packages for this lab session.
{tidyverse} will be for all things workflow and {stevedata} will
have the data sets we’ll be using today.
library(tidyverse)
#> ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
#> ✔ dplyr 1.1.1 ✔ readr 2.1.4
#> ✔ forcats 1.0.0 ✔ stringr 1.5.0
#> ✔ ggplot2 3.5.1 ✔ tibble 3.2.1
#> ✔ lubridate 1.9.2 ✔ tidyr 1.3.0
#> ✔ purrr 1.0.1
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag() masks stats::lag()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
library(stevedata)
# For those of you without `{tidyverse}`, do this:
# library(dplyr)
# library(tibble)
# library(magrittr)
# library(forcats)
# library(ggplot2)
Building Toward Multiple Regression
Last time we had a lab, we just focused on bivariate linear model with
fake data that we created. The goal of that exercise was to show you
what the linear model looked like when you had maximum control over the
model parameters. We’ll use some actual data this time. This is a survey
data set from the United Kingdom in 2018-19, largely probing individual
attitudes toward immigration. You can find out more about this data set
by typing ?ESS9GB into Rstudio. You can also go
here for a web
version of the codebook.
ESS9GB
#> # A tibble: 1,905 × 19
#> name essround edition idno cntry region brncntr stintrvw endintrvw
#> <chr> <dbl> <chr> <dbl> <chr> <chr> <dbl> <date> <date>
#> 1 ESS9e01_2 9 1.2 39 GB West Mi… 1 2018-09-11 2018-09-11
#> 2 ESS9e01_2 9 1.2 135 GB South W… 1 2018-09-07 2018-09-07
#> 3 ESS9e01_2 9 1.2 142 GB South E… 1 2018-11-03 2018-11-03
#> 4 ESS9e01_2 9 1.2 146 GB Norther… 1 2018-10-06 2018-10-17
#> 5 ESS9e01_2 9 1.2 164 GB Norther… 1 2018-10-31 2018-10-31
#> 6 ESS9e01_2 9 1.2 191 GB Norther… 1 2018-10-27 2018-10-27
#> 7 ESS9e01_2 9 1.2 213 GB South W… 1 2018-11-08 2018-11-08
#> 8 ESS9e01_2 9 1.2 238 GB London 1 2019-01-31 2019-01-31
#> 9 ESS9e01_2 9 1.2 245 GB East of… 1 2018-09-07 2018-09-07
#> 10 ESS9e01_2 9 1.2 265 GB East Mi… 1 2019-02-10 2019-02-10
#> # ℹ 1,895 more rows
#> # ℹ 10 more variables: imbgeco <dbl>, imueclt <dbl>, imwbcnt <dbl>,
#> # immigsent <dbl>, agea <dbl>, female <dbl>, eduyrs <dbl>, uempla <dbl>,
#> # hinctnta <dbl>, lrscale <dbl>
You can also see read some blog posts where I make considerable use of these data here:
- What Do We Know About British Attitudes Toward Immigration? A Pedagogical Exercise of Sample Inference and Regression
- How Should You Think About Your Priors for a Bayesian Analysis?
Understand that some of that is slightly more complex than what we’ll be doing here, but I’d rather inundate you with things to look at and read rather than give you nothing at all.
Our primary dependent variable in this model will be the immigsent
variable, which is an additive index of three variables also included in
the data set. These prompts, verbatim, each range from 0 to 10 and
ask 1) Would you say it is generally bad or good for the United
Kingdom’s economy that people come to live here from other countries?
(imbgeco), 2) And… would you say that the United Kingdom’s cultural
life is generally undermined or enriched by people coming to live here
from other countries? (imueclt), and 3) Is the United Kingdom made a
worse or a better place to live by people coming to live here from other
countries? (imwbcnt). The immigsent variable simply adds all three
together, resulting in a scale that ranges from 0 to 30. You can
interpret 0 as being maximally anti-immigrant/immigration and 30 being
maximally pro-immigrant/immigration. Higher values = more
pro-immigration sentiment. Let’s build toward multiple regression by
starting in the simple bivariate, like we did in lecture. We’ll start by
exploring an uncontroversial argument that we should expect
pro-immigration sentiment to be much lower in North East than other
parts of the United Kingdom. Why “North East”? This is the region where
Newcastle is. Newcastle, rightly or wrongly, has a reputation of being
“Brexit
Central”.
We have the means to explore this with the region variable. Let’s take
a look at it.
ESS9GB %>% distinct(region)
#> # A tibble: 12 × 1
#> region
#> <chr>
#> 1 West Midlands (England)
#> 2 South West (England)
#> 3 South East (England)
#> 4 Northern Ireland
#> 5 London
#> 6 East of England
#> 7 East Midlands (England)
#> 8 North West (England)
#> 9 Scotland
#> 10 Yorkshire and the Humber
#> 11 North East (England)
#> 12 Wales
Perfect. I see I have 12 familiar regions to me in the data to explore, but I have no “North East” dummy variable. No matter, it’s a simple matter to create one like this.
ESS9GB %>%
mutate(northeast = ifelse(region == "North East (England)", 1, 0)) -> Data
Note: I’m creating a new data frame here for convenience sake.
Now let’s do a simple regression, regressing the immigration sentiment variable on whether the respondent is in the North East.
M1 <- lm(immigsent ~ northeast, data=Data)
summary(M1)
#>
#> Call:
#> lm(formula = immigsent ~ northeast, data = Data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -17.0235 -4.0235 0.9765 4.9765 15.3495
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 17.0235 0.1668 102.051 < 2e-16 ***
#> northeast -2.3730 0.7070 -3.357 0.000805 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 6.972 on 1848 degrees of freedom
#> (55 observations deleted due to missingness)
#> Multiple R-squared: 0.00606, Adjusted R-squared: 0.005522
#> F-statistic: 11.27 on 1 and 1848 DF, p-value: 0.0008051
By the way, in a super simple case like this where y is continuous and x is binary, this is basically what the t-test will tell you as well.
t.test(immigsent ~ northeast, Data)
#>
#> Welch Two Sample t-test
#>
#> data: immigsent by northeast
#> t = 3.3873, df = 114.62, p-value = 0.0009679
#> alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
#> 95 percent confidence interval:
#> 0.9852718 3.7606949
#> sample estimates:
#> mean in group 0 mean in group 1
#> 17.02347 14.65049
In this simple difference of means, the mean immigration sentiment where
northeast is 0 is 17.02. The mean immigration sentiment where
northeast is 1 is 14.65. The difference between those two numbers is
basically the regression coefficient. It’s the “North East” effect,
which basically decreases immigration sentiment by about 2.37. That
effect is highly unlikely to be zero. You knew that because we went over
statistical significance and null hypothesis testing. You also know
that, one assumes, from just kind of eye-balling the United Kingdom with
a polite curiosity. Again, “rightly or wrongly.”
You can also do the same thing and look for differences between Scotland and not-Scotland.
Data %>%
mutate(scotland = ifelse(region == "Scotland", 1, 0)) -> Data
M2 <- lm(immigsent ~ scotland, Data)
summary(M2)
#>
#> Call:
#> lm(formula = immigsent ~ scotland, data = Data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -18.5030 -4.7335 0.2665 5.2665 13.2665
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 16.7335 0.1699 98.47 <2e-16 ***
#> scotland 1.7695 0.5690 3.11 0.0019 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 6.975 on 1848 degrees of freedom
#> (55 observations deleted due to missingness)
#> Multiple R-squared: 0.005206, Adjusted R-squared: 0.004668
#> F-statistic: 9.671 on 1 and 1848 DF, p-value: 0.0019
The model here suggests that pro-immigration sentiment in not-Scotland is 16.73. The “Scotland” effect increases pro-immigration sentiment by 1.76. The t statistic suggest that if the true differences between Scotland and not-Scotland is 0, what we got would have been observed about .19% of the time, on average.
What if we wanted to tease out more information for all regions? This would be a kind of “fixed effects” analysis, which is a somewhat misleading and confusing way of saying “take a categorical variable, and create a series of dummy variables from it.” You could do this manually, or you can have R do it for you.
M3 <- lm(immigsent ~ factor(region), Data)
summary(M3)
#>
#> Call:
#> lm(formula = immigsent ~ factor(region), data = Data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -18.503 -4.503 0.497 5.349 15.350
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 16.4296 0.5811 28.275 < 2e-16 ***
#> factor(region)East of England 0.9694 0.7655 1.266 0.20558
#> factor(region)London 1.5526 0.8751 1.774 0.07619 .
#> factor(region)North East (England) -1.7791 0.8962 -1.985 0.04727 *
#> factor(region)North West (England) -0.9162 0.7428 -1.233 0.21755
#> factor(region)Northern Ireland 0.9038 1.0662 0.848 0.39674
#> factor(region)Scotland 2.0735 0.7926 2.616 0.00897 **
#> factor(region)South East (England) 1.4281 0.7129 2.003 0.04531 *
#> factor(region)South West (England) 1.1347 0.7781 1.458 0.14496
#> factor(region)Wales -0.5905 0.9427 -0.626 0.53115
#> factor(region)West Midlands (England) -0.8676 0.8567 -1.013 0.31131
#> factor(region)Yorkshire and the Humber 0.2043 0.7744 0.264 0.79194
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 6.924 on 1838 degrees of freedom
#> (55 observations deleted due to missingness)
#> Multiple R-squared: 0.02502, Adjusted R-squared: 0.01919
#> F-statistic: 4.289 on 11 and 1838 DF, p-value: 2.437e-06
I want to stop right here and explain what this procedure is doing. First, you have 12 regions, but you get 11 regression coefficients. In this procedure, something must be a baseline. Second, if you don’t give R any guidance, the “baseline” becomes whatever is first in alphabetical order. In this case, that is “East Midlands (England)”, which is the region where Leicester and Nottingham are (if Premier League squads may help orient you). What this “fixed effects” communicates, then, is the difference between East of England (i.e. where Norwich, Essex and Cambridge are) relative to East Midlands (and if there is a discernible difference), the difference between London and East Midlands (and if it’s discernible), the difference between North East and East Midlands (and if it’s discernible), and so on. Here, we’d suggest discernible differences relative to the baseline of London, North East, Scotland, and South East (i.e. where Brighton, Canterbury, and Dover are). Pro-immigration sentiment is higher in London, South East, and Scotland relative to East Midlands and lower in North East relative to East Midlands.
A few other things. For one, you could basically tease much of this out through doing a comparison of means. This procedure doesn’t demonstrate “significance”, but calculating standard errors and creating lower and upper bounds around that mean will illustrate a little bit more about what the regression model is telling you.
Data %>%
summarize(mean = mean(immigsent, na.rm=T),
sd = sd(immigsent, na.rm=T),
n = n(),
se = sd/sqrt(n()),
lwr = mean - se,
upr = mean + se,
.by = region) %>%
data.frame
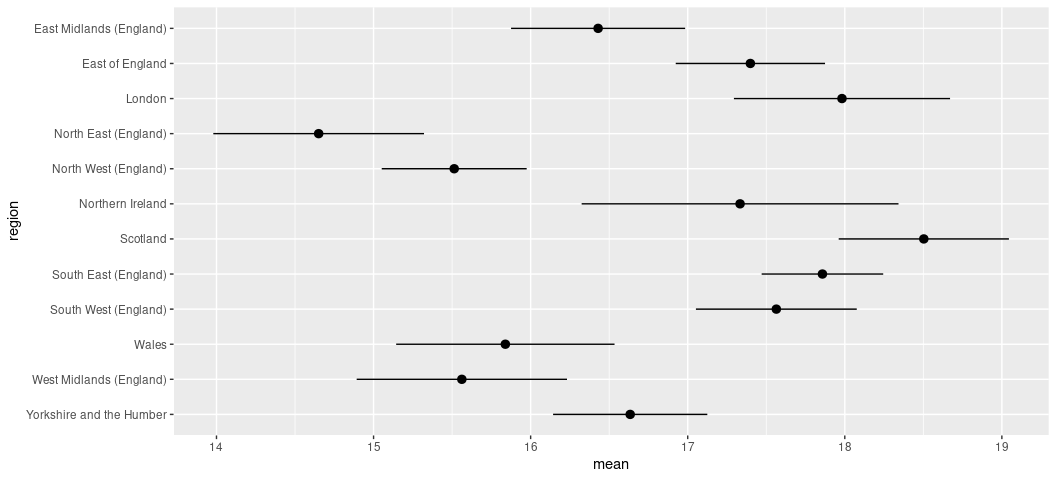
#> region mean sd n se lwr upr
#> 1 West Midlands (England) 15.56198 7.485422 125 0.6695165 14.89247 16.23150
#> 2 South West (England) 17.56425 7.001609 187 0.5120084 17.05224 18.07625
#> 3 South East (England) 17.85765 6.566774 288 0.3869509 17.47070 18.24460
#> 4 Northern Ireland 17.33333 7.941879 62 1.0086197 16.32471 18.34195
#> 5 London 17.98214 7.345995 114 0.6880155 17.29413 18.67016
#> 6 East of England 17.39896 6.704429 199 0.4752644 16.92370 17.87423
#> 7 East Midlands (England) 16.42958 6.764947 149 0.5542061 15.87537 16.98378
#> 8 North West (England) 15.51339 6.936599 226 0.4614157 15.05198 15.97481
#> 9 Scotland 18.50303 7.043960 169 0.5418431 17.96119 19.04487
#> 10 Yorkshire and the Humber 16.63388 6.767111 190 0.4909378 16.14294 17.12482
#> 11 North East (England) 14.65049 6.905111 106 0.6706837 13.97980 15.32117
#> 12 Wales 15.83908 6.594348 90 0.6951054 15.14398 16.53419
Graphing it will help.
Data %>%
summarize(mean = mean(immigsent, na.rm=T),
sd = sd(immigsent, na.rm=T),
n = n(),
se = sd/sqrt(n()),
lwr = mean - se,
upr = mean + se,
.by = region) %>%
# The next two lines are super-hacky ways of making the plot read in order.
arrange(desc(region)) %>%
mutate(region = fct_inorder(region)) %>%
# Notice below: region is x-axis, mean is y-axis, and I've outlined that I
# want the `lwr` and `upr` columns to be mins and maxes for what's coming
# next...
ggplot(., aes(region, mean, ymin=lwr, ymax=upr)) +
# ...the point-range. This will create a dot at `mean` and bounds
# that correspond with the ymin and ymax variables.
geom_pointrange() +
# Put your coords down flip them and reverse them.
coord_flip()
What if you wanted to make London the baseline? You could manually
create your own dummy variables, or you can turn that “region” variable
into a more informative factor through the use of the {forcats}
package (which is loaded with {tidyverse}). Let’s use fct_relevel()
for this purpose. Using fct_relevel() in the way I do below, I’m
basically telling R that this new region2 variable is a factor and
it’s specific order is 1) London and 2) after that, I don’t care, and
just proceed alphabetically as you wish.
Data %>%
mutate(region2 = fct_relevel(region, "London")) -> Data
Data %>% summary
#> name essround edition idno
#> Length:1905 Min. :9 Length:1905 Min. : 39
#> Class :character 1st Qu.:9 Class :character 1st Qu.:12350
#> Mode :character Median :9 Mode :character Median :24627
#> Mean :9 Mean :24597
#> 3rd Qu.:9 3rd Qu.:37088
#> Max. :9 Max. :48626
#>
#> cntry region brncntr stintrvw
#> Length:1905 Length:1905 Min. :1 Min. :2018-09-01
#> Class :character Class :character 1st Qu.:1 1st Qu.:2018-09-29
#> Mode :character Mode :character Median :1 Median :2018-10-18
#> Mean :1 Mean :2018-10-27
#> 3rd Qu.:1 3rd Qu.:2018-11-12
#> Max. :1 Max. :2019-02-16
#>
#> endintrvw imbgeco imueclt imwbcnt
#> Min. :2018-09-01 Min. : 0.000 Min. : 0.0 Min. : 0.000
#> 1st Qu.:2018-10-01 1st Qu.: 5.000 1st Qu.: 4.0 1st Qu.: 4.000
#> Median :2018-10-18 Median : 6.000 Median : 6.0 Median : 5.000
#> Mean :2018-10-27 Mean : 5.698 Mean : 5.7 Mean : 5.447
#> 3rd Qu.:2018-11-12 3rd Qu.: 7.000 3rd Qu.: 8.0 3rd Qu.: 7.000
#> Max. :2019-02-16 Max. :10.000 Max. :10.0 Max. :10.000
#> NA's :4 NA's :18 NA's :28 NA's :29
#> immigsent agea female eduyrs
#> Min. : 0.00 Min. :15.00 Min. :0.0000 Min. : 3.00
#> 1st Qu.:12.25 1st Qu.:39.00 1st Qu.:0.0000 1st Qu.:11.00
#> Median :17.00 Median :55.00 Median :1.0000 Median :13.00
#> Mean :16.89 Mean :53.67 Mean :0.5412 Mean :14.05
#> 3rd Qu.:22.00 3rd Qu.:69.00 3rd Qu.:1.0000 3rd Qu.:16.00
#> Max. :30.00 Max. :90.00 Max. :1.0000 Max. :41.00
#> NA's :55 NA's :12 NA's :12
#> uempla hinctnta lrscale northeast
#> Min. :0.00000 Min. : 1.000 Min. : 0.000 Min. :0.00000
#> 1st Qu.:0.00000 1st Qu.: 2.000 1st Qu.: 4.000 1st Qu.:0.00000
#> Median :0.00000 Median : 5.000 Median : 5.000 Median :0.00000
#> Mean :0.01995 Mean : 5.171 Mean : 4.961 Mean :0.05564
#> 3rd Qu.:0.00000 3rd Qu.: 8.000 3rd Qu.: 6.000 3rd Qu.:0.00000
#> Max. :1.00000 Max. :10.000 Max. :10.000 Max. :1.00000
#> NA's :290 NA's :179
#> scotland region2
#> Min. :0.00000 South East (England) :288
#> 1st Qu.:0.00000 North West (England) :226
#> Median :0.00000 East of England :199
#> Mean :0.08871 Yorkshire and the Humber:190
#> 3rd Qu.:0.00000 South West (England) :187
#> Max. :1.00000 Scotland :169
#> (Other) :646
Now, let’s do this again.
M4 <- lm(immigsent ~ region2, Data)
summary(M4)
#>
#> Call:
#> lm(formula = immigsent ~ region2, data = Data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -18.503 -4.503 0.497 5.349 15.350
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 17.9821 0.6543 27.484 < 2e-16 ***
#> region2East Midlands (England) -1.5526 0.8751 -1.774 0.076188 .
#> region2East of England -0.5832 0.8225 -0.709 0.478393
#> region2North East (England) -3.3317 0.9453 -3.524 0.000435 ***
#> region2North West (England) -2.4687 0.8013 -3.081 0.002095 **
#> region2Northern Ireland -0.6488 1.1078 -0.586 0.558158
#> region2Scotland 0.5209 0.8477 0.614 0.538998
#> region2South East (England) -0.1245 0.7738 -0.161 0.872196
#> region2South West (England) -0.4179 0.8342 -0.501 0.616473
#> region2Wales -2.1431 0.9895 -2.166 0.030460 *
#> region2West Midlands (England) -2.4202 0.9079 -2.666 0.007752 **
#> region2Yorkshire and the Humber -1.3483 0.8307 -1.623 0.104755
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 6.924 on 1838 degrees of freedom
#> (55 observations deleted due to missingness)
#> Multiple R-squared: 0.02502, Adjusted R-squared: 0.01919
#> F-statistic: 4.289 on 11 and 1838 DF, p-value: 2.437e-06
This time, you’re benchmarking any comparisons to London. Just because there’s no difference between London and Scotland here doesn’t mean there’s no difference between Scotland and East Midlands. What you do with so-called “fixed effects” depends on what you want to accomplish. Does it matter that something is the baseline? If so, make it the baseline and compare everything else to it. Do you not care, and you’re just doing this because you want to partial out these potential categorical effects while you focus on some other regressors? Then don’t bother with the details, because it’s mostly immaterial to what you want to accomplish.
Multiple Regression
Now, let’s a do a multiple regression. Let’s see if we can’t regress the immigration sentiment variable on the Scotland dummy variable, whether the respondent is a woman, and the respondent’s ideology on a 0-10 scale where 0 is the most to the right, and 10 is the most to the left. You knew how to do this in the bivariate case, but what do you do to the formula when you have multiple independent variables? Simple as this:
M5 <- lm(immigsent ~ scotland + female + lrscale, Data)
summary(M5)
#>
#> Call:
#> lm(formula = immigsent ~ scotland + female + lrscale, data = Data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -19.9503 -4.1965 0.7144 4.9605 14.0774
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 20.38127 0.49521 41.156 < 2e-16 ***
#> scotland 1.45623 0.57385 2.538 0.0112 *
#> female -0.43092 0.32923 -1.309 0.1908
#> lrscale -0.63696 0.08515 -7.480 1.19e-13 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 6.757 on 1687 degrees of freedom
#> (214 observations deleted due to missingness)
#> Multiple R-squared: 0.03758, Adjusted R-squared: 0.03587
#> F-statistic: 21.96 on 3 and 1687 DF, p-value: 6.007e-14
In other words: separate however many x variables you want in the
equation with a + sign. The formula above could be read as “using the
lm() function, regress immigsent on scotland and female and
lrscale from the Data data set.” Let’s walk through the basic
takeaways from the model:
- The estimated pro-immigration sentiment for a man, not residing in Scotland, who is furthest to the political left is 20.38. In this case, the y-intercept actually exists. This parameter isn’t total nonsense, at least on paper.
- Partialing out everything else in the model (“ceteris paribus”), the effect of going from not-Scotland to “Scotland” increases pro-immigration sentiment by 1.45 points on our scale. If the true “Scotland effect” were 0, we’d expect to have observed this effect, on average, about 1.12% of the time. We’d suggest that “Scotland effect” is statistically significant.
- The partial effect of being a woman versus a man (“ceteris paribus”) is to decrease pro-immigration sentiment by -.43 points. However, the corresponding t-statistic and p-value suggests that such an effect would be observed about 19% of the time if there truly was no effect. Thus, the parameters are consistent with a null hypothesis of no relationship between pro-immigration sentiment and gender. We can’t discern a difference between men and women exist here with respect to this outcome variable.
- Partialing out the Scotland effect and potential gender differences, we see an unsurprising effect of ideology on pro-immigration sentiment. Higher levels of ideological affinity with the right coincide with lower levels of pro-immigration sentiment. The unit effect is -.63 and that effect is incidentally the most precise in the model. There is a clear ideology effect in our model.
Interactive Effects
Let’s walk through the issue of what to do when you think there might be
an interactive relationship among x and z in their relationship with
y. I’m going to keep this example simple. We noticed there were no
gender differences, but is that because it depends on ideology? Let’s
see, and notice how we’re going to see it below. When you want to see if
two (or more, but let’s focus on just two) things interact, you put an
asterisk (*) between the variables in the right-hand side of the
equation. Like this:
M7 <- lm(immigsent ~ scotland + female*lrscale, Data)
summary(M7)
#>
#> Call:
#> lm(formula = immigsent ~ scotland + female * lrscale, data = Data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -19.6005 -4.2097 0.7691 5.1946 14.7929
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 21.1989 0.6717 31.562 < 2e-16 ***
#> scotland 1.4440 0.5735 2.518 0.0119 *
#> female -1.9481 0.9046 -2.154 0.0314 *
#> lrscale -0.7992 0.1239 -6.449 1.47e-10 ***
#> female:lrscale 0.3064 0.1702 1.801 0.0720 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 6.752 on 1686 degrees of freedom
#> (214 observations deleted due to missingness)
#> Multiple R-squared: 0.03942, Adjusted R-squared: 0.03715
#> F-statistic: 17.3 on 4 and 1686 DF, p-value: 6.435e-14
Notice that two variables we interacted produced three regression
coefficients. The female coefficient is the gender difference when
lrscale is 0 (i.e. the respondent is furthest to the left). The
lrscale coefficient is the effect of increasing ideological affinity
to the right when female is 0 (i.e. the effect of ideology on men).
The female:lrscale communicates a way of thinking about how the two
interact with each other, and whether that interaction is “significant”.
Here, it is (albeit at the .10 level). The “Scotland effect” variable is
not affected by this and is still an “all else equal” partial effect.
I want to use this as an illustrative case. Be careful in how you interpret your interactions, and how you model them. We got lucky here that that the data have naturally occurring 0s, but what is “0”—and whether there’s a 0 at all—will influence what exactly the regression summary tells you. For example, let’s center the data so that 0 is the people in the middle of the scale. Observe:
Data %>%
mutate(c_lrscale = lrscale - 5) -> Data
Data %>%
distinct(lrscale, c_lrscale) %>%
arrange(lrscale)
#> # A tibble: 12 × 2
#> lrscale c_lrscale
#> <dbl> <dbl>
#> 1 0 -5
#> 2 1 -4
#> 3 2 -3
#> 4 3 -2
#> 5 4 -1
#> 6 5 0
#> 7 6 1
#> 8 7 2
#> 9 8 3
#> 10 9 4
#> 11 10 5
#> 12 NA NA
Take very quick inventory of what this did. We took the raw data and subtracted 5 from it. Now, 0 are people who would place themselves in the ideological middle. 5 are the people furthest to the right and -5 are the people furthest to the left. We didn’t really “change” 0, as much as we shifted it.
Now, watch.
M8 <- lm(immigsent ~ scotland + female*c_lrscale, Data)
summary(M8)
#>
#> Call:
#> lm(formula = immigsent ~ scotland + female * c_lrscale, data = Data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -19.6005 -4.2097 0.7691 5.1946 14.7929
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 17.2030 0.2426 70.914 < 2e-16 ***
#> scotland 1.4440 0.5735 2.518 0.0119 *
#> female -0.4161 0.3291 -1.264 0.2063
#> c_lrscale -0.7992 0.1239 -6.449 1.47e-10 ***
#> female:c_lrscale 0.3064 0.1702 1.801 0.0720 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 6.752 on 1686 degrees of freedom
#> (214 observations deleted due to missingness)
#> Multiple R-squared: 0.03942, Adjusted R-squared: 0.03715
#> F-statistic: 17.3 on 4 and 1686 DF, p-value: 6.435e-14
Compare this to the output of M7. Notice how the gender dummy variable
isn’t significant? Except, again, you have to be careful because the
female dummy is now the difference between men and women for those in
the middle, not the far left. The interactive coefficient didn’t move,
but the gender variable did. The ideology constituent effect didn’t move
because men are still the baseline. Just be careful about what’s
actually happening in an interaction.
I wanted to close with a caveat about interactions. Just because the overall interactive effect is insignificant, or just because component terms of the interaction are insignificant, doesn’t mean there isn’t something potentially interesting happening in your interactions. If the interaction is statistically significant, you should definitely look at it to see what the interaction looks like. If it’s insignificant, you should still look at it. After all, you’re the one that felt compelled to interact two things. Go look at what you did just to see for yourself.
Here’s what we’ll do. We’ll create a simple prediction grid. Let the
ideology variable be either 0 (furthest to the left), 5 (in the middle),
or 10 (furthest to the right). Let the female variable range from 0
to 1. Then, given the model we estimated, we’re going to get predictions
from the model and standard errors around those predictions. Let the
Scotland effect be 0 for convenience sake. Then, we’ll create
conceivable lower and upper bounds around these estimates and graph
them.
Note: it’s killing me to not ask you to install {modelr} for this, but
you should absolutely install {modelr} for this. It makes it way less
tedious.
tibble(lrscale = c(0, 5, 10, 0, 5, 10),
female = c(0,0,0,1,1,1),
scotland = 0) -> newdat
newdat # Look at our hypothetical data/prediction grid.
#> # A tibble: 6 × 3
#> lrscale female scotland
#> <dbl> <dbl> <dbl>
#> 1 0 0 0
#> 2 5 0 0
#> 3 10 0 0
#> 4 0 1 0
#> 5 5 1 0
#> 6 10 1 0
Preds <- predict(M7, newdata = newdat, se.fit = TRUE)
Preds # Look at our predictions.
#> $fit
#> 1 2 3 4 5 6
#> 21.19887 17.20297 13.20707 19.25074 16.78684 14.32294
#>
#> $se.fit
#> 1 2 3 4 5 6
#> 0.6716501 0.2425894 0.6591887 0.6158585 0.2340980 0.6426349
#>
#> $df
#> [1] 1686
#>
#> $residual.scale
#> [1] 6.752303
Preds %>% as_tibble() %>% # Coerce to a tibble, and...
# bind_cols to the prediction grid/hypothetical data, and...
bind_cols(newdat, .) %>%
# select just what we want, to look at it...
select(lrscale:se.fit)
#> # A tibble: 6 × 5
#> lrscale female scotland fit se.fit
#> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0 0 0 21.2 0.672
#> 2 5 0 0 17.2 0.243
#> 3 10 0 0 13.2 0.659
#> 4 0 1 0 19.3 0.616
#> 5 5 1 0 16.8 0.234
#> 6 10 1 0 14.3 0.643
Since I can see that performed how I wanted it to. Let’s make it pretty.
Preds %>% as_tibble() %>%
bind_cols(newdat, .) %>%
select(lrscale:se.fit) %>%
# Okay, there's going to be some hackiness (sic). First, we're going to create
# lower and upper bounds that are 90% intervals around +/- the standard error.
# Next, we're going to create a categorical variable from the female variable
# in a way that's super obvious. Next. We're going to create a categorical
# variable from the `lrscale` variable (ideo_lbl) that adds more intuitive
# labels. The \n you see there forces a linebreak for legibility in the label.
# You'll see what it does. Using the fct_inorder() forces it to be ordered
# because, otherwise, it would display 0, 10, 5 (i.e. furthest, furthest,
# middle) because of the alphabetical order. Because our data are already
# ordered, this is just a shortcut/cheat code to do what we want to do. In
# this case, it's because I know y'all might help to see the left in red and
# the right in blue.
mutate(lwr = fit - 1.645*se.fit,
upr = fit + 1.645*se.fit,
gndr_lbl = ifelse(female == 0, "Men", "Women"),
ideo_lbl = case_when(
lrscale == 0 ~ "Furthest\nLeft",
lrscale == 5 ~ "Middle",
lrscale == 10 ~ "Furthest\nRight"
),
ideo_lbl = fct_inorder(ideo_lbl)) %>%
ggplot(.,aes(gndr_lbl, fit, ymin=lwr, ymax=upr, color=ideo_lbl)) +
geom_pointrange(position = position_dodge(width = .1)) +
coord_flip() +
theme_minimal() +
labs(x = "", y = "Estimated Pro-Immigration Sentiment (with 90% Bounds)",
color = "")
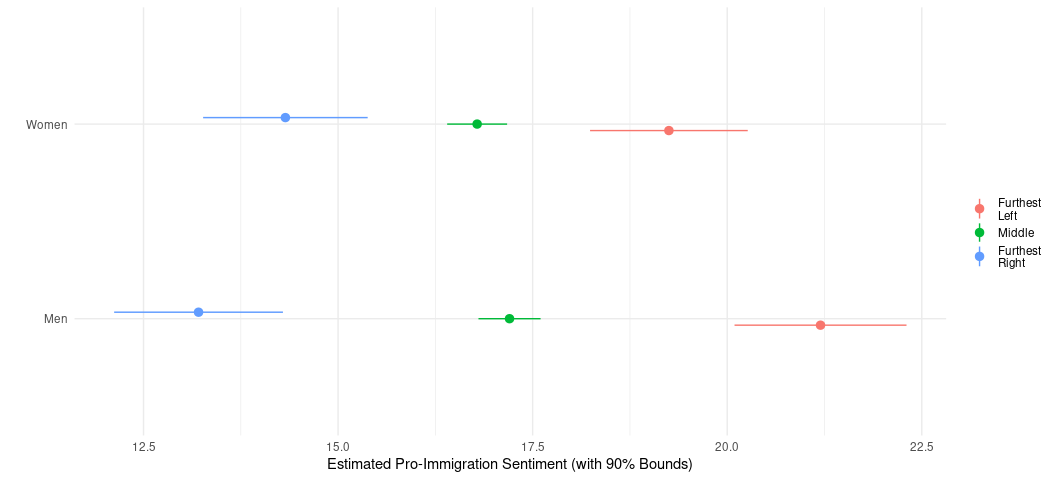
What this tells me: the effect of increasing ideology on pro-immigration sentiment is stronger for the men than it is the women. For women furthest to the left, their mean pro-immigration sentiment is 19.3. Furthest to the right: 14.3. That’s a min-max difference of about 5 points. For the men: the estimated pro-immigration sentiment for non-Scottish dudes furthest to the left is 21.2, which is interestingly higher than the women furthest to the left. However, the estimated pro-immigration sentiment for the men furthest to the right is 13.2. That’s a min-max difference of 8 points. Kinda cool, and kinda interesting as I’m doing this on the fly for the sake of this class.
There, is I suppose, an alternate interpretation that is largely consistent with the data but communicates a different mechanism happening here. In the above interpretation, I largely channeled the effect of ideology through men and women. There could also be a story to tell about why there is an apparent gender difference among those furthest to the left but no real gender differences among those furthest to the right. In this potential interpretation, there is a potential gender mechanism that’s being clustered on ideology, and why is it that the men and women are more like each other on this matter (in this simple model) among the most right whereas they are more different among those most to the left.
I’ll defer to you to make sense of the findings as you see fit, and why you think you see what you see (provided you treat such an obviously simple model as gospel truth about the UK population at this point in time). No matter, always look at your data. You might find something cool in there.