Some Basics of Descriptive Statistics
This lab script will introduce students to some basic elements of descriptive statistics. Nothing here will be too exotic and assumes at least some rudimentary knowledge of measures of central tendency. The recurring theme here is you should never trust a summary statistic without first looking at your data. The best diagnostics are visual, and ultimately anticipatory.
R Packages/Data for This Session
You should’ve already installed the R packages for this lab session.
{tidyverse} will be for all things workflow and {stevedata} will be
for the toy data sets. Let’s load those libraries now. The order doesn’t
really matter here.
library(stevedata)
library(tidyverse)
#> ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
#> ✔ dplyr 1.1.2 ✔ readr 2.1.4
#> ✔ forcats 1.0.0 ✔ stringr 1.5.0
#> ✔ ggplot2 3.5.1 ✔ tibble 3.2.1
#> ✔ lubridate 1.9.2 ✔ tidyr 1.3.0
#> ✔ purrr 1.0.2
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag() masks stats::lag()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
If, for some reason, you don’t want to load {tidyverse} (i.e. you
might be one of my past students that had some issues with
{systemfonts}), here are the component packages we’ll be using. Just
“uncomment” (sic) these four lines of code and execute them.
# library(dplyr)
# library(tidyr)
# library(magrittr)
# library(ggplot2)
In your R session, please look up the documentation for the data set to
get a better idea as to what each variables are. Here’s how I want you
to think about this. You the smart researcher know that the race
column in gss_spending is a categorical variable where 1 = white
people, 2 = black people, and 3 = people who self-identify with another
race. However, your dumb computer and dumb R program don’t know that.
They just see numbers. You know the underlying information they
communicate. At least, you should know it.
I like to think my toy data sets are well annotated. If you want to read
the documentation file for one of my toy data sets, put a ? before the
object name in the console. This should fire up the documentation file
in another Rstudio pane (i.e. where the plots typically go).
We’ll be using three toy data sets in this session. The first is American attitudes toward national spending in the General Social Survey (2018). The second is a sample of macroeconomic data from the Penn World Table (from the previous lab session). The third data set are attitudes about the justifiability of taking a bribe in the World Values Survey.
# Check out documentation.
?gss_spending
?pwt_sample
?wvs_justifbribe
Identifying Modes and Medians
If you know a variable of interest is discrete (i.e. it only has a finite set of responses), your tools for assessing central tendency are limited. There are two types here: unordered-categorical and ordered-categorical. Unordered-categorical variables are cases where numeric values communicate only differences. While we all learned in elementary school that 2 is greater than 1, we gloss over that it’s also true that 2 does not equal 1. They are distinct from each other. Sometimes, we have a variable where that’s all the underlying information available. Unordered-categorical variables are quite common in the social sciences, even as we don’t necessarily like to acknowledge them as such (because they are information-poor).
Getting Modes for Unordered-Categorical Variables
For example, the race variable in the gss_spending is
unordered-categorical. We can see from the documentation that 1 = white,
2 = black, and 3 = other. However, we cannot say that 2 (black) is
greater than 1 (white) nor can we say that 3 (other) is two greater than
1 (white). Numerically, we know that’s true, but that’s just not the
information communicated in this variable. All we can say is that 2 != 1
(which is also true, but not something we really learned in grade school
math). Likewise, white != black.
Under those conditions, the most we can do with unordered-categorical variables is to get the mode as an information-poor measure of central tendency. The mode refers to the most commonly occurring value. R doesn’t have a built-in mode function. That’s understandable since modes aren’t very useful information and you can get it through other means. However, we can write a simple function to extract the mode from a variable.
# R doesn't have a built-in mode function. So let's write one.
getmode <- function(v) {
uniqv <- unique(v)
uniqv[which.max(tabulate(match(v, uniqv)))]
}
getmode(gss_spending$race)
#> [1] 1
gss_spending %>% summarize(mode = getmode(race))
#> # A tibble: 1 × 1
#> mode
#> <dbl>
#> 1 1
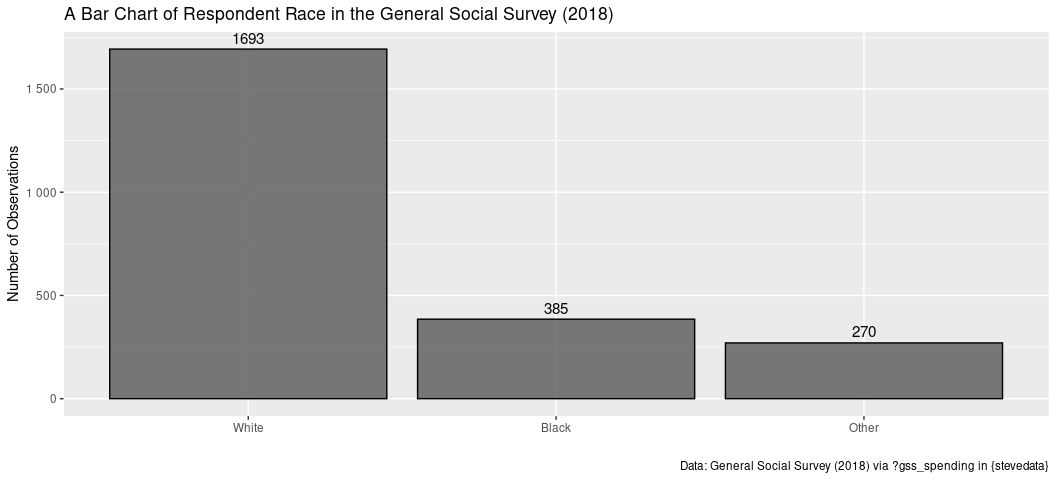
This tells us that there are more white people in the sample than there are people identifying with any other race. This is not surprising. We already know that white people are about 75% of the U.S. population (about 60% disentangling out Hispanic [like me] as an ethnicity).
There are more creative means to get the mode and get more information
to boot. For example, here’s a “tidy” approach that leans on
group_by() and count().
gss_spending %>%
count(race) %>%
# ^ you could stop here, but let's have more fun.
# create more information...
mutate(race_lab = c("White", "Black", "Other"),
prop = n/sum(n)) %>%
# creatively arrange the order of columns
select(race, race_lab, everything())
#> # A tibble: 3 × 4
#> race race_lab n prop
#> <dbl> <chr> <int> <dbl>
#> 1 1 White 1693 0.721
#> 2 2 Black 385 0.164
#> 3 3 Other 270 0.115
You could also graph this information. Do note I encourage using a
fancier {ggplot2} theme (like my theme_steve()) in {stevethemes},
but this will do for this purpose.
gss_spending %>%
count(race) %>%
ggplot(., aes(as.factor(race), n)) +
geom_bar(color="black", alpha=0.8, stat="identity") +
scale_y_continuous(labels = scales::comma_format(big.mark = " ")) +
scale_x_discrete(labels = c("White","Black","Other")) +
geom_text(aes(label=n), vjust=-.5, colour="black",
position=position_dodge(.9), size=4) +
labs(x = "",
y = "Number of Observations",
caption = "Data: General Social Survey (2018) via ?gss_spending in {stevedata}",
title = "A Bar Chart of Respondent Race in the General Social Survey (2018)")
Getting Medians for Ordered-Categorical Variables
The second kind of discrete variable is called “ordered-categorical.” These are variables where increasing (or decreasing) values communicate “more” (or “less”) of some phenomenon being measured, but the distance is inexact or even vague. Logically, ordered-categorical variables say 3 > 1 where unordered-categorical variables say 3 != 1, though these variables do not tell us that 3 is two greater than 1.
Ordered-categorical variables appear in several forms, but perhaps the most common is a Likert item. Likert items give a statement to a respondent and prompt the respondent to respond with their level of agreement. This is often a five-point scale with responses of “strongly disagree” (1), “disagree” (2), “neither agree nor disagree” (3), “agree” (4), and “strongly agree” (5). If someone says they “strongly agree” with the prompt, we can reasonably say they are in more agreement with the prompt than someone who just “agrees”. But how much more are they in agreement with the prompt? We can’t say because the only difference between “strongly agree” and “agree” is a vague magnifier of “strongly”. In other words, 5 > 4, but 5 is not one greater than 4 in this context.
The most precise measure for central tendency for ordered-categorical
variables is the median. The median refers to the middlemost value where
half of the observations are above it and half of the observations are
below it. Fortunately, R has a built-in median() function. One
caution, though: if you have NAs in the column for which you want the
median, the output will return an NA. You can suppress that at your
discretion with na.rm=T.
Here’s an example of the highest degree obtained by the respondent in
the gss_spending data frame. Educational attainment is routinely
measured like this. Higher values = more educational attainment, which
broadly means “more education.” In the gss_spending data frame, the
degree variable assumes values of 0 (did not graduate high school), 1
(completed high school), 2 (completed junior college), 3 (completed
four-year bachelor’s equivalent), 4 (graduate degree). This would be the
median of that variable.
median(gss_spending$degree, na.rm=T)
#> [1] 1
That’s unsurprising the extent to which we know only about 35% of Americans have at least a four-year college diploma.
You can also calculate a cumulative percentage to get the same information. The row where the cumulative percentage of responses exceeds 50% is the row that contains the median.
gss_spending %>%
count(degree) %>%
mutate(degree_lab = c("Did Not Graduate HS", "High School", "Junior College",
"Bachelor Degree", "Graduate Degree"),
prop = n/sum(n),
cumperc = cumsum(prop)*100) %>%
select(degree, degree_lab, everything())
#> # A tibble: 5 × 5
#> degree degree_lab n prop cumperc
#> <dbl> <chr> <int> <dbl> <dbl>
#> 1 0 Did Not Graduate HS 262 0.112 11.2
#> 2 1 High School 1178 0.502 61.3
#> 3 2 Junior College 196 0.0835 69.7
#> 4 3 Bachelor Degree 465 0.198 89.5
#> 5 4 Graduate Degree 247 0.105 100
Identifying the Mean (and Standard Deviation)
Means are what would want in most applications, provided your data are interval and could be plausibly described by the mean. The mean is the statistical “average” of the data. They are reserved for data where numerical values communicate exact differences.
For example, let’s go back to our pwt_sample data and calculate the
mean for the real GDP variable for each year, as well as the standard
deviation. Like the median() function, mean() and sd() throws up
an NA if there are missing observations. We can suppress that the same
way.
pwt_sample %>%
summarize(mean_rgdpna = mean(rgdpna, na.rm=T),
sd_rdgpna = sd(rgdpna, na.rm=T),
.by = year)
#> # A tibble: 70 × 3
#> year mean_rgdpna sd_rdgpna
#> <int> <dbl> <dbl>
#> 1 1950 283633. 540370.
#> 2 1951 279853. 560884.
#> 3 1952 291816. 584176.
#> 4 1953 306871. 612224.
#> 5 1954 315290. 610298.
#> 6 1955 336535. 654213.
#> 7 1956 349391. 669280.
#> 8 1957 361120. 684516.
#> 9 1958 366450. 681544.
#> 10 1959 387933. 728801.
#> # ℹ 60 more rows
Remember to always look at your data before saying anything with confidence about them, but a standard deviation that is larger than a mean is usually a good indicator of a large, large spread in the data. Since we’re dealing with GDP data you’ll have the GDPs of the United States juxtaposed to Greece and Iceland, at least in this sample.
You can also graph this if you wanted to see mean real GDP over time for these 22 countries.
pwt_sample %>%
summarize(meanrgdp = mean(rgdpna, na.rm=T),
.by = year) %>%
mutate(meanrgdpb = meanrgdp/1000) %>%
ggplot(.,aes(year, meanrgdpb)) +
geom_line() +
scale_x_continuous(breaks = seq(1950, 2020, by = 10)) +
scale_y_continuous(labels = scales::dollar_format()) +
labs(x = "",
y = "Average Real GDP (in Constant 2017 National Prices, in Billion 2017 USD)",
caption = "Data: Penn World Table (v. 10.0) via ?pwt_sample in {stevedata}",
title = "Average Real GDP for 22 Rich Countries, 1950-2019",
subtitle = "The average real GDP in 2017 was over 2.3 trillion dollars, which should seem super sketchy.")
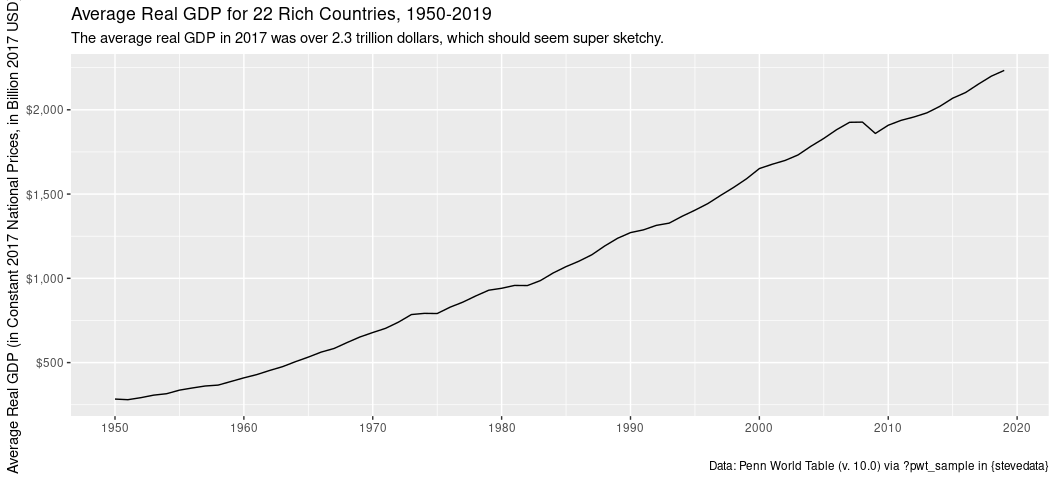
Nothing looks terribly amiss in that line chart, per se. You see a little recession effect. You see the “lostness” of the 1970s, at least a little. However, something is. Did you notice that the average real GDP for these 22 countries in 2019 was over 2 trillion dollars? Something seems fishy about that, because it is. These data are 22 select rich countries, but the United States has an enormous GDP among even those select rich countries. I use these data to underscore a basic problem with the arithmetic mean for continuous variables: it is very sensitive to skew (here: right skew). The U.S. is a clear anomaly among these select rich countries. Indeed, it looks like the U.S. is four times the size of the next biggest economy in 2019 and is about as big as the next seven biggest economies (in these data) combined.
pwt_sample %>%
filter(year == 2019) %>%
mutate(rgdpb = rgdpna/1000) %>%
select(country, year, rgdpb) %>%
arrange(-rgdpb) %>%
data.frame(.)
#> country year rgdpb
#> 1 United States of America 2019 20563.59200
#> 2 Japan 2019 5095.62350
#> 3 Germany 2019 4312.88600
#> 4 United Kingdom 2019 3015.58275
#> 5 France 2019 2963.64075
#> 6 Italy 2019 2467.12875
#> 7 Spain 2019 1895.66900
#> 8 Canada 2019 1873.62525
#> 9 Australia 2019 1315.58125
#> 10 Netherlands 2019 960.96438
#> 11 Switzerland 2019 648.57969
#> 12 Belgium 2019 534.58587
#> 13 Sweden 2019 531.64131
#> 14 Austria 2019 476.65728
#> 15 Ireland 2019 472.53750
#> 16 Chile 2019 443.55059
#> 17 Norway 2019 377.59797
#> 18 Portugal 2019 329.15109
#> 19 Denmark 2019 311.12172
#> 20 Greece 2019 289.44516
#> 21 Finland 2019 247.93434
#> 22 Iceland 2019 17.63955
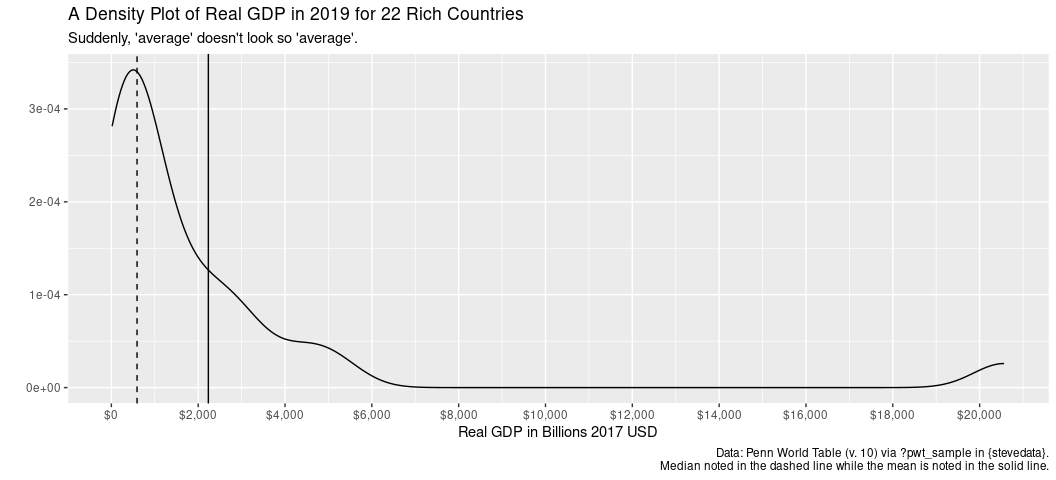
This is why economic indicators are often expressed by the median rather than the mean. The mean is sensitive to outlier observations whereas the median is robust to them. When you describe your interval-level variables, do a quick comparison between the median and the mean to see how far off the median is from the mean. Where the distance is large, it points in the problem of outlier observations.
pwt_sample %>%
filter(year == 2019) %>%
mutate(rgdpb = rgdpna/1000) %>%
ggplot(.,aes(rgdpb)) +
geom_density() +
geom_vline(aes(xintercept = median(rgdpb, na.rm = T)), linetype="dashed") +
geom_vline(aes(xintercept = mean(rgdpb, na.rm = T))) +
scale_x_continuous(breaks = seq(0, 20000,by=2000),
labels = scales::dollar_format()) +
labs(title = "A Density Plot of Real GDP in 2019 for 22 Rich Countries",
x = "Real GDP in Billions 2017 USD",
y = "",
caption = "Data: Penn World Table (v. 10) via ?pwt_sample in {stevedata}.\nMedian noted in the dashed line while the mean is noted in the solid line.",
subtitle = "Suddenly, 'average' doesn't look so 'average'.")
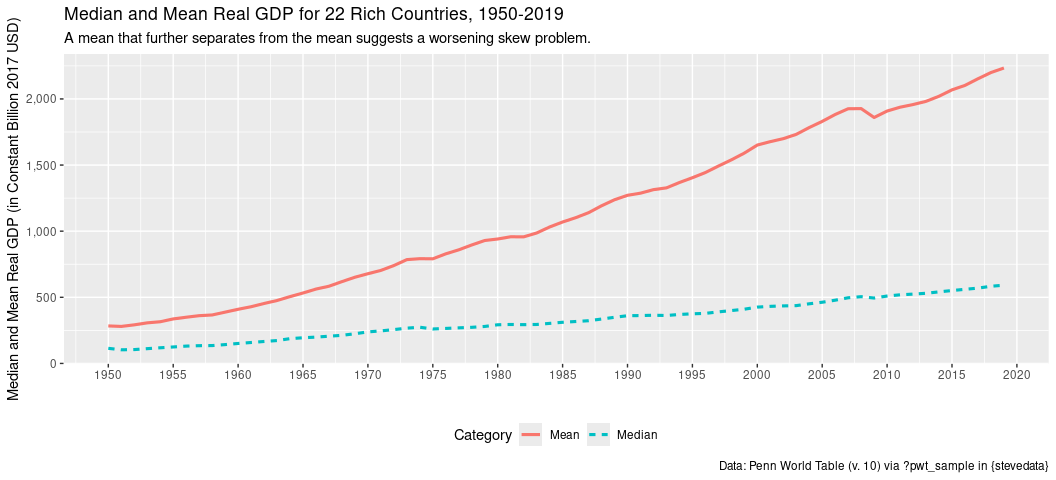
Here’s another way of looking at it: plotting the yearly mean against the yearly median. The extent to which the mean further separates from the median implies a skew problem that is getting worse over time.
pwt_sample %>%
mutate(rgdpb = rgdpna/1000) %>%
summarize(Median = median(rgdpb, na.rm=T),
Mean = mean(rgdpb, na.rm=T),
.by = year) %>%
gather(Category, value, Median:Mean, -year) %>%
ggplot(.,aes(year,value, color=Category, linetype=Category)) +
geom_line(linewidth=1.1) +
scale_x_continuous(breaks = seq(1950, 2020, by =5)) +
scale_y_continuous(labels = scales::comma) +
theme(legend.position = "bottom") + labs(x = "",
y = "Median and Mean Real GDP (in Constant Billion 2017 USD)",
caption = "Data: Penn World Table (v. 10) via ?pwt_sample in {stevedata}",
title = "Median and Mean Real GDP for 22 Rich Countries, 1950-2019",
subtitle = "A mean that further separates from the mean suggests a worsening skew problem.")
An Aside: On “Dummy” Variables
I want to dedicate a special comment here to what are commonly called “dummy” variables. “Dummy” variables (aka binary variables) are variables that take on just two values—functionally 0 or 1. While some dummies have an intuitive order (e.g. “democracy” vs. “not democracy” implies “more democracy”), the phenomenon being measured is strictly “there” or “not there.” This means they are a unique subset of nominal variables, effectively saying they are unordered-categorical with just two categories (“there” or “not there”, “success” vs. “fail”).
That said, I liken them to the carbon or water of the variable world in that they behave in interesting ways and have some interesting peculiarities/properties. With respect to central tendency, the mode and median of a dummy variable will be the same value and the mean will communicate the proportion of 1s. This assumes that your dummies are recoded to 0/1, which you should always do. Dummies are often provided to you as 1/2. Always recode those.
Let’s see what this looks like with the sex variable in
gss_spending. sex is a numeric vector for the respondent’s sex,
either female (1) or male (0).
gss_spending %>%
# where sex = 1 for women, 0 for men
summarize(mode = getmode(sex),
median = median(sex),
mean = mean(sex))
#> # A tibble: 1 × 3
#> mode median mean
#> <dbl> <dbl> <dbl>
#> 1 1 1 0.552
The above tells me that there are more women than men in the data (the mode), the middlemost observation is a woman on this dummy variable (the median), and that about 55.2% of the observations are women (the mean).
An Aside: Ordinal or Interval? Or Something Else?
Practitioners love to treat technically ordinal data as interval. There’s more you can do with an interval-level variable than you can with an ordinal (ordered-categorical) variable. However, you have to ask yourself just how advisable this is. For example, take yourself back to college when you just turned 21. Are you truly one year older than your 20-year-old friend when it comes to identification at the off-campus bar? Legally you are, but you might just be three weeks older than your 20-year-old friend. Here, you have information loss in the form of days/weeks. Is someone who lists their yearly income at $50,010 truly 10 dollars richer than someone who lists their yearly income at $50,000? Legally they are (i.e. Uncle Sam cares about dollars, not cents), but you have information loss in the form of cents.
That said, we often describe age by reference to an average and we can (provided there are no major issues of skew) understand an average income. Certainly, practitioners would go-go-gadget a mean on those variables. Here’s a general rule of thumb that I haven’t seen anyone formalize out loud (even if there’s supporting scholarship you’ll read for this) but nonetheless guides how we do this. First, check the number of possible values. Second, check the skew. If you have at least 5—I would caution at least 7, even to 10)—distinct values, you can start to think of it as interval. However, check the distribution of the variable. If you have a major skew problem, don’t treat it as interval and consider another approach to modeling your variable.
Age is technically ordinal, but there are typically a wide number of distinct ages in survey data spanning from 18 to the 80s and beyond. Therein, differences between observations are granular enough that means with decimals make some sense. Below, the mean is about 48.97. You can reasonably conceptualize that as an average age of 48 that is 97% of the way to turning 49.
gss_spending %>%
summarize(mean = mean(age, na.rm=T),
median = median(age, na.rm=T),
distinct = n_distinct(age))
#> # A tibble: 1 × 3
#> mean median distinct
#> <dbl> <dbl> <int>
#> 1 49.0 48 73
Caveat, naturally: don’t try to explain age as some outcome if you’re thinking ahead to a linear model. Age is a linear function of time. :P
The sumnat variable in my gss_spending data frame summarizes all
responses to spending toward all programs from the ordinal scale
provided in the original prompts (again: ?gss_spending for more). It
has a small skew problem to the left, but it’s cast across 33 different
values.
gss_spending %>%
summarize(mean = mean(sumnat, na.rm=T),
median = median(sumnat, na.rm=T),
distinct = n_distinct(sumnat))
#> # A tibble: 1 × 3
#> mean median distinct
#> <dbl> <dbl> <int>
#> 1 6.37 7 33
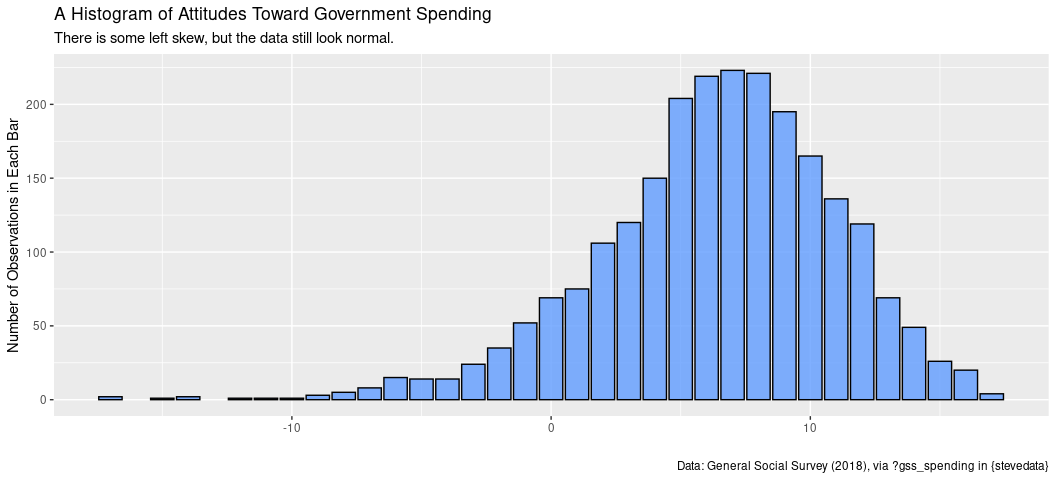
A diagnostic graph doesn’t suggest a major problem for skew either. It’s not a disservice to this variable to summarize it with a mean.
gss_spending %>%
ggplot(.,aes(sumnat)) +
geom_bar(alpha=0.8, fill="#619cff",color="black") +
labs(title = "A Histogram of Attitudes Toward Government Spending",
subtitle = "There is some left skew, but the data still look normal.",
caption = "Data: General Social Survey (2018), via ?gss_spending in {stevedata}",
x = "", y = "Number of Observations in Each Bar")
Some variables, however, are too damn ugly to think of as interval the extent to which you want informative means and so on. Here’s an example from the World Values Survey regarding the justifiability of taking a bribe. This is part of a series of World Values Survey items where the researcher lists various behaviors (e.g. abortion, divorce, homosexuality, here: taking a bribe) and the respondent lists how justifiable they think it is on a 1-10 scale. 10 = always justifiable. 1 = never justifiable. Here would be the summary statistics.
wvs_justifbribe %>%
na.omit %>%
summarize(mean = mean(f117, na.rm=T),
median = median(f117, na.rm=T),
distinct = n_distinct(f117))
#> # A tibble: 1 × 3
#> mean median distinct
#> <dbl> <dbl> <int>
#> 1 1.80 1 10
I’m anticipating a problem here. The mean is almost one off the median with just 10 distinct values. A graph will bring the problem in full light.
wvs_justifbribe %>%
count(f117) %>%
na.omit %>% # count() will also summarize the NAs, which we don't want.
ggplot(.,aes(as.factor(f117), n)) +
geom_bar(stat="identity", alpha=0.8, color="black") +
scale_x_discrete(labels=c("Never Justifiable", "2", "3", "4",
"5", "6", "7", "8", "9", "Always Justifiable")) +
scale_y_continuous(labels = scales::comma_format(big.mark = " ")) +
geom_text(aes(label=n), vjust=-.5, colour="black",
position=position_dodge(.9), size=4) +
labs(y = "Number of Observations in Particular Response",
x = "",
title = "The Justifiability of Taking a Bribe in the World Values Survey, 1981-2016",
caption = "Data: World Values Survey (1981-2016), via ?wvs_justifbribe in {stevedata}",
subtitle = "There are just 10 different responses in this variable with a huge right skew.")
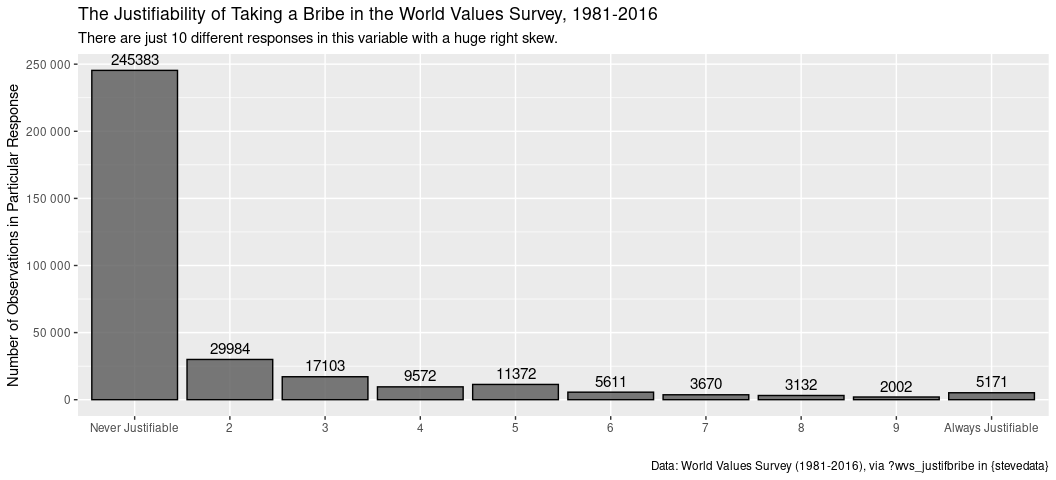
Here’s what I recommend doing in an admittedly extreme situation like this. First, no matter the 10 different values, don’t ask for a mean from this. A mean won’t be terribly informative because the data have a huge skew problem and a finite scale of possible responses. Two, the median is at the most you can get here, but I’d caution against treating it as useful information as well. Again, there’s a huge skew. Third, for an extreme situation like this where more than 70% of the data are in just one response, collapse the variable into a dummy variable. In this case, 0 = taking a bribe is never justifiable and 1 = taking a bribe is at least somewhat justifiable. I did something like this with the exact question; others have too. Here’s how you’d basically do it. Your data basically look like this.
wvs_justifbribe
#> # A tibble: 348,532 × 6
#> s002 s003 country s020 uid f117
#> <dbl> <dbl> <chr> <dbl> <int> <dbl>
#> 1 1 32 Argentina 1984 1 1
#> 2 1 32 Argentina 1984 2 1
#> 3 1 32 Argentina 1984 3 1
#> 4 1 32 Argentina 1984 4 4
#> 5 1 32 Argentina 1984 5 5
#> 6 1 32 Argentina 1984 6 5
#> 7 1 32 Argentina 1984 7 5
#> 8 1 32 Argentina 1984 8 4
#> 9 1 32 Argentina 1984 9 1
#> 10 1 32 Argentina 1984 10 1
#> # ℹ 348,522 more rows
wvs_justifbribe %>%
mutate(never_justifiable = ifelse(f117 == 1, 1, 0),
somewhat_justifiable = ifelse(f117 == 1, 0, 1)) %>%
select(uid, f117, never_justifiable:ncol(.))
#> # A tibble: 348,532 × 4
#> uid f117 never_justifiable somewhat_justifiable
#> <int> <dbl> <dbl> <dbl>
#> 1 1 1 1 0
#> 2 2 1 1 0
#> 3 3 1 1 0
#> 4 4 4 0 1
#> 5 5 5 0 1
#> 6 6 5 0 1
#> 7 7 5 0 1
#> 8 8 4 0 1
#> 9 9 1 1 0
#> 10 10 1 1 0
#> # ℹ 348,522 more rows
You want to use the mutate() function to create a dummy variable
whereby if f117 is 1, it’s 0. If it’s greater than 1, code it as 1.
Let’s use the mutate() wrapper to create a new bribe_dummy variable
that has this information. Pay careful attention to what the
case_when() function is doing in this context.
# Take our data frame, and...
wvs_justifbribe %>%
# use the mutate() function to create a new column, using case_when(), where...
mutate(bribe_dummy = case_when(
# if f117 == 1, it's 0
f117 == 1 ~ 0,
# if it's f117 > 1 (or %in% c(2:10)), it's 1
f117 > 1 ~ 1,
# if it's anything else (here: NA), keep it as NA.
TRUE ~ NA_real_
)) -> Data # Create a new data object for now.
Let’s see what this did.
Data %>%
distinct(f117, bribe_dummy)
#> # A tibble: 11 × 2
#> f117 bribe_dummy
#> <dbl> <dbl>
#> 1 1 0
#> 2 4 1
#> 3 5 1
#> 4 6 1
#> 5 2 1
#> 6 3 1
#> 7 NA NA
#> 8 7 1
#> 9 8 1
#> 10 9 1
#> 11 10 1
Congrats on recoding your first variable! Notice too how you created a
new column that did not overwrite the original, so you can always
troubleshoot what you did to see if you messed up somewhere. Btw, since
I know this is going to be something you’ll need to know to do for a
homework question I’ll ask, let’s assume we’re interested in those that
are NA here. NA can mean multiple things, but what if we just assume
that they’re people that are withholding what they think about taking a
bribe and we want to perhaps understand that as a kind of dependent
variable? Here’s how we’d do that.
# Taking our data frame, and...
Data %>%
# ...using mutate() to create a new column in the data where,
# using case_when()
mutate(missing_f117 = case_when(
# if it's missing, it's a 1
is.na(f117) ~ 1,
# if it's anything else (`TRUE` in case_when() speak), it's 0
TRUE ~ 0
)) -> Data # assign to object
Let’s see what this did.
Data %>%
distinct(f117, missing_f117)
#> # A tibble: 11 × 2
#> f117 missing_f117
#> <dbl> <dbl>
#> 1 1 0
#> 2 4 0
#> 3 5 0
#> 4 6 0
#> 5 2 0
#> 6 3 0
#> 7 NA 1
#> 8 7 0
#> 9 8 0
#> 10 9 0
#> 11 10 0